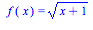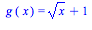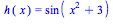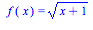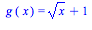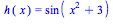Write-ups of
the problems below
are due Monday Oct. 9
Monday
Oct 2
We did:
A.2: proved Theorems 1,4iii. We will take Theorem 5 for granted.
Solve,
write up and turn in: In Sec. 2.5 problems 1, 2, 5(explain here why
you are allowed to simplify the fraction when calculating the limit),
9, 17
(You do not need to use the epsilon-delta definition of limits,
use the properties of limits. We have worked so hard to prove
them...now we can use them!)
Bonus
problem (extra 3 points) Prove problem 3a from Friday Sept. 28 by
induction on the degree of the polynomial.
Hint: write polynomials of
degree n in the form P(x)=cnx^n+cn-1x^(n-1)+...+c1x+c0.
and note that P(x)=cnx^n+polynomial of
degree (n-1).
Tuesday
Oct 3
Plan:
Sec. 2.5:
sin x/x ->1 (as x->0),
lateral limits, cases when limits do not exist. A.2: Theorem 6.
Solve,
write up and turn in: Sec. 2.5
2, 4, 8, 10, 14, 15,
19a,g,f, 20 c,d,g
Wednesday
Oct 4
We did
today: we calculated limits, we proved Theorem 6 of A2 (the
squeeze theorem) and discussed applications, we defined
lim as x->infinity.
Solve,
write up and turn in: Sec. 2.5 (revisit yesterday's problems
and) 18 c,d,e,f and also:
1. a) Does the function
cos x have a limit as x->infinity? Explain.
b) Does the
function cos (1/x) have a limit as x->0? Explain.
c) Show that the limit of xcos (1/x) as x->0 is 0.
2. Let f(x) be a bounded
function (this means that there are some numbers b,B so that
b<f(x)<B for all x).
Show that the limit of the function xf(x) as x->0 exists and equals
0.
Bonus problem (extra 3p.): Write down the definition of "the
limit of f(x) as x goes to negative infinity equals L".
Note: For Tuesday's assignment I
wrote by mistake Sec. 2.6 instead of 2.5.
Thursday
Oct 5
Topics:
Continuity Sec. 2.6 and A.2 Theorems 7,8,9,10. We defined
composition.
Solve: 1a,b,e
Solve,
write up and turn in: Sec. 2.6 (page 79)1 f,g,h and
3. Consider the function
f(x)=sin(3x)/x if x is not 0 and f(0)=C.
For which number C the function f(x) is continuous on the whole real
line?
Bonus (extra 5 points) Consider
the function f(x)=0 if x is rational and
=1 if x is irrational.
Show that this function is discontinuous at all the points.
At which points is xf(x) continuous?
Hint: please read first the
Remarks at the bottom of page 5 of Bounds.
The implication is that:
any real number can be approached through rationals only, or through
irrationals only.
Friday
Oct 6
Topics:
Sec. A2 Theorem 11. Continuous functions on closed intervals - Sec.
A.3: Theorem 1 (no proof required, but,
attention math majors and minors: please do
read the proof), Theorem 2.
Solve,
write up and turn in: 4. Write the following functions as a
composition of two simpler functions:
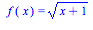
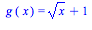
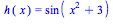
Also: Sec. 2.6
(page 79/80) 1 e (and explain which theorems you used and how), and also
*15 c, 16 b,c, 21, 22, 29 to all of which answering the
additional questions:
explain (if it is the case) if max/min necessarily exists,
and if those functions have a supremum, or infimum,
on the stated intervals, explain why and what are their values *